
我是蓝晞,一枚持续分享数学小知识的数学爱好者,点击右上方【关注】,你想看的数学干货都在这里!
学习数学其实没有太难,难的是“建造”好属于自己的数学思维,所以我经常说:“想要学好数学,要坚持每天训练自己的数学思维,不要觉得题型简单会做就行,要从多方面去思考,有没其他更好的解题思路。”
这是一道小学的数学几何图形题,几何图形组合挺简单的,但学生哭着说:“这实在是太难了”。
真的有这么难吗?也许只是数学的解题思维没有掌握好,无法巧用数学思路应用解题。
今天在这里与大家分享一道几何图形的一题多解,希望在这里总有一种解题思路能对你有所帮助。
题目:如图,图形由四边形ABCD、BEFC、DCGH均为长方形堆积而成,且D、C、F三点共线,B、C、G三点也共线,连接BD、GF,长方形DCHG的面积为12cm²,长方形BEFC的面积为32cm²,△CFG的面积为12cm²,求阴影部分的面积是多少?
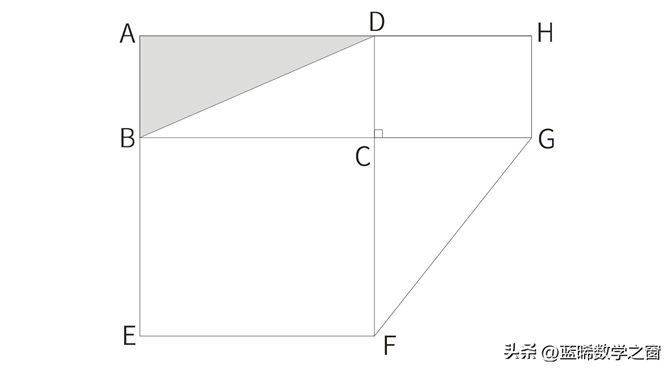

图形补全法
延长HG与延长EF相交于点P,如图所示:
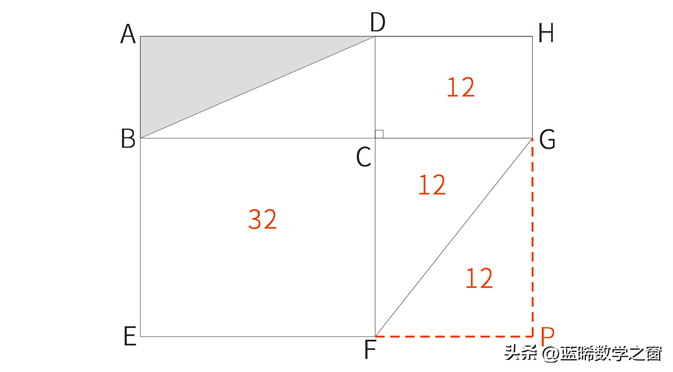
根据题意,FG为长方形CFPG的对角线,
所以S长方形CFPG=2×12=24(cm²)
因为长方形BEFC与长方形CFPG的高相等,则有:
==
同理可得:
=
=
S长方形ABCD=×12=16(cm²)
根据长方形一半模型可得:
S阴影=S长方形ABCD
=×16
=8(cm²)


直接观察法(作辅助线法)
构建风筝模型解题思路
连接BF、DG,如图所示:
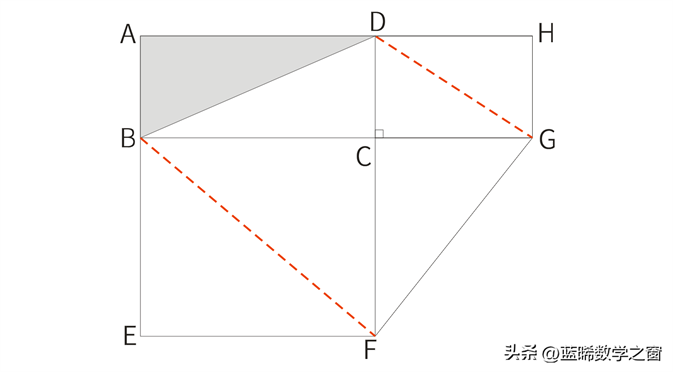
根据题意,可得:
S△BCF=S长方形BEFC
=×32
=16(cm²)
S△DCG=S长方形DCGH
=×12
=6(cm²)
根据风筝模型原理,可得:
S△BCF×S△DCG=S△BCD×S△CFG
16×6=S△BCD×12
S△BCD=16×6÷12=8(cm²)
因此可得:
S阴影=S△BCD=8(cm²)


列方程法
设BC=a,CD=b,如图所示:
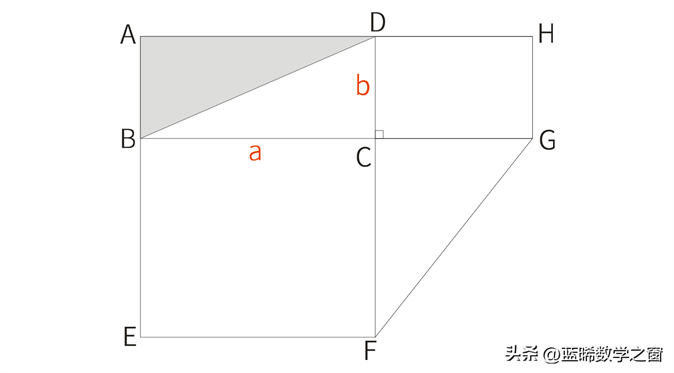
由题意可得:S长方形DCGH=S△CFG
因为:S长方形DCGH=CG×b=12
S△CFG=CG×CF=12
所以可得:CF=2b
又因为,S长方形BEFC=BC×CF=32,即a×2b=32
则有:ab=16
由此可得:
S阴影=S长方形ABCD
=ab
=×16
=8(cm²)


图形补全法
(面积比例法)
延长HG与延长EF相交于点P,设长方形的面积分别为:S1、S2、S3、S4,如图所示:
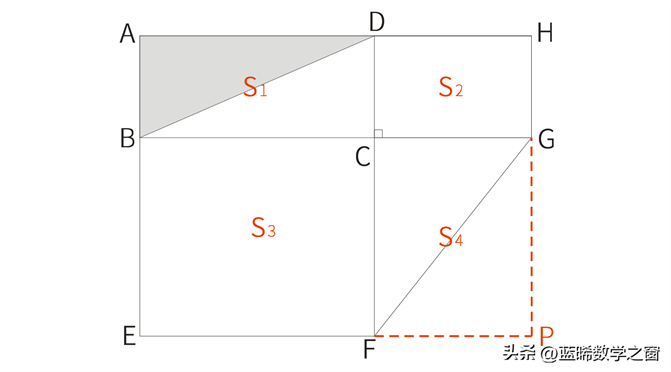
根据题意,FG为长方形CFPG的对角线,所以S1(S长方形CFPG)=2×12=24(cm²)
根据面积比例法(由风筝模型同理可推得)
S1×S4=S2×S3
S1×24=12×32
S1=12×32÷24=16
由此可得:
S阴影=S长方形ABCD
=S1
=×16
=8(cm²)
分享解题思路,若有错误,欢迎大家指导修正,有更好的解题思路,大家也可以一起分享,共同学习进步

 17攻略
17攻略






